Luminosity
Luminosity is the intrinsic brightness of an object. It is measured in the units of energy per time or watts (W)
For example, the Sun radiates \(4\times10^{26}\)W. Solar parameters are given special units. This amount of luminosity is called solar luminosity and is denoted by \(L_\odot\). $$L_\odot=4\times10^{26}\text{W}$$
In astronomy, it is common to use cgs units. \(1\text{W} = 10^7\text{erg s}^{-1}\). $$L_\odot=4\times10^{33}\text{erg s}^{-1}$$ The luminosity of our galaxy is about \(10^{11}L_\odot\)Flux
The amount of radiation received by an observer who is at some distance away from the source of luminosity is the flux received by them.Naturally, this follows an inverse square law (see diagram below).
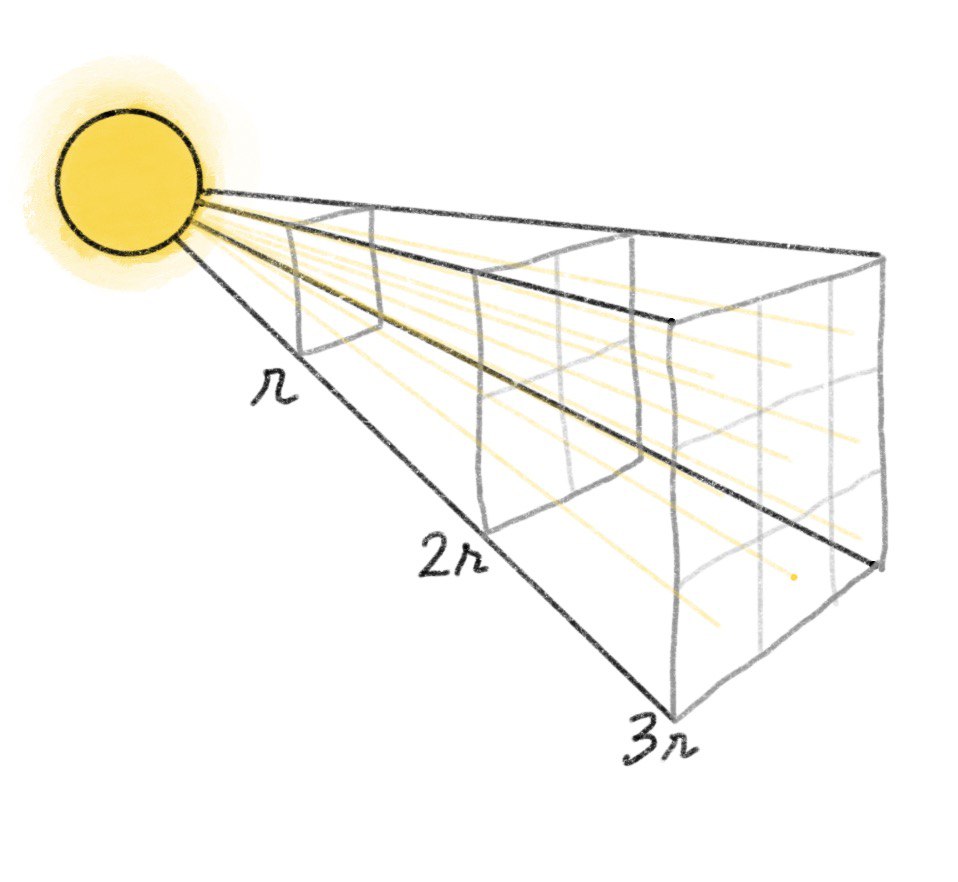
Units of flux: energy per unit area.
Apparent & Absolute Magnitudes
Apparent Magnitude
Human eyes are actually designed to percieve brightness logarithmically. It is therefore more convenient to have a logarithmic scale to measure brightness instead of a linear scale.
Hipparchus was a Greek astronomer in second century who catalogued stars visible to the naked eye. He divided stars into 6 categories based on their apparent magnitudes (m). The apparent magnitude of \(m=1\) would be the brightest and \(m=6\) would be the faintest star.
Astronomers today use a similar scale even today! \(m=6\) is the limit of the naked eye. This is the faintest we can see without any aid. However, today, much fainter stars have been observed with telescopes.
Relation between the flux (brightness) of two objects and their apparent magnitudes is: $$m_1 -m_2 = 2.5 \log_{10} \frac{F_2}{F_1}$$ This scale is defined in such a way that a brightness difference of 100 corresponds to 5 magnitudes.So, a star of magnitude 1 is
\(2.512\) times brighter than a star of magnitude 2
\(2.512^2 = 6.3\) times brighter than a star of magnitude 3
\(2.512^3 = 16\) times brighter than a star of magnitude 4
\(2.512^4 = 40\) times brighter than a star of magnitude 5
\(2.512^5 = 100\) times brighter than a star of magnitude 6
As expected, the difference of 5 magnitude means a \(100\times\) difference in brightness.
Note: Smaller magnitude => brighter object
How much will be the apparent magnitude if the current apparent magnitude is \(m_\odot=4.83\)?
Solution:
Since the flux is now twice the value, we have \(m_1 = m_\odot, \ m_2 = ? F_2 = 2F, \ F_1 = F\) we solve the following:
\[ \begin{align*} m_1 - m_2 & = 2.5 \log_{10} \frac{F_2}{F_1} \\ m_\odot - m_2 & = 2.5 \log_{10} \frac{2F}{F} \\ 4.83 - m_2 & = 2.5 \log_{10} 2 \\ m_2 & = 4.83 - 2.5 \log_{10} 2 \\ m_2 & = 4.07 \end{align*} \] ∴ the apparent magnitude of two Suns would be 4.07. A smaller value since it would be brighter.
The magnitude decrease of roughly 0.76 (i.e., 4.83-4.07) corresponds to doubling of the flux or brightness.
Absolute Magnitude
Since apparent magnitude is related to the flux received, it does not tell us anything about the true brightness (luminosity). A faint star very close to us could easily appear brighter than a much brighter star which is far-far away.
Wouldn't it be convenient if we could place all the stars on the equal footing?
That's why we define the absolute magnitude (M) of a star.
This is the apparent magnitude of a star when it is placed \(10\) pc away from us.
This definition makes provides the formula:
$$m-M=2.5 \log{\frac{\frac{L}{4\pi r^2}}{\frac{L}{4\pi 10^2}}}$$
Note: \(r\) is in pc and L dosen't change (it's intrinsic, dosen't depend on the distance). Simplifying,
$$m-M=5\log{\frac{r}{10}}$$
The interesting this to note is that this formula can be used to find the absolute magnitude of a source, when its distance is known. Distances can be known using the parallax
of a source which is relatively easy to measure.
Conversely, if we know the absolute magnitude of a source (say it is a known type star), we can get a measure of its distance by simple comparing the apparent and absolute magnitudes using the above formula.
Distance Modulus
Having known the apparent and absolute magnitude of a star, we can infer how far it is from us.$$m-M=5\log{\frac{r}{10}}$$ $$r = 10\times10^{(m-M)/5} \text{ pc}$$
Use the following calculators to find the distance to any star given its \(m\) and \(M\).
r (distance) using m (apparent) and M (absolute) magnitudes
Enter the apparent magnitude \(m\) and absolute magnitude \(m\) to calculate \(r\)
Try substituting these values in the input fields. You should get 1 AU for the distance 😉
Distance \(r\)